Topology in action

Let’s say I put a sphere in front of you. I’m sure you could go through and tell me the basic facts and formulas surrounding it, many if which containing Pi. And even better, if you were a bit more fluent in maths, you could go further and start telling me about the geometry of the shape, say how the gradient had to disappear at a certain point or an assortment of many other things. But if we dive a little deeper into pure maths, it starts getting a little more complicated. When labels like Hausdorff get casually thrown about (meaning you can always separate two distinct points with an open boundary, which you certainly can do on a sphere!) it can really build up and become quite hard, especially if someone then puts in front of you two spheres stuck together. This is where the study of topology comes in and starts helping out, allowing us to start to categorise certain spaces without having to worry about all the small details that could catch you out.

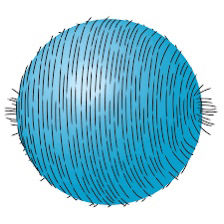
Topology is certainly found in the purer side of maths, generally seen as one of the more abstract modules to be taking at undergraduate level (as seen by the exam scores). But thinking of it just as some far away concept disconnected with the rest of the world would be foolish. Thinking back to what I said before about gradient fields on a sphere, this is more commonly known in maths as the “Hairy Ball Theorem” named as such as if you had a ball of hair, you wouldn’t be able to smooth it all out without a cow’s lick. And in mathematical terms it means that a continuous vector field has to disappear at a certain point. And maybe not readily apparent but this comes up in loads of places, the most obvious of which is that two points on the Earth will always have the exact temperature!

But moving to Biology we see a lot more applications, even as early as in A-level study. Just thinking about how a protein will fold is all to do with the topological properties of them. DNA is a bit more complex understandably, with more base pairs it becomes incredibly flexible, able to bend into many shapes, but like topological spaces this flexible has limits. It doesn’t pass through itself nor tear, so it allows us to start applying our theorems to it. A key one of these is Knot theory, which of course is the study of knots. Knots in maths are defined as having no open ends and being complex, which helpfully is exactly like DNA! As you hopefully know, its coiled form has no open ends, and in order to untangle it we have to go through the process of cutting at double points. The amount of times this is needed to untangle is called the unknotting number in topology and this mathematical modelling of the process allows biologists to move away from the microscope and still get a more accurate look on what’s happening.

 Written by Tom Murphy